How to Merge Two Sorted Arrays

1. Introduction

In this tutorial, we're going to learn how to merge two sorted arrays into a single sorted array.

2. Problem

Let's understand the problem. We have two sorted arrays and we would like to merge them into one.

3. Algorithm

When we analyze the problem, it's quite easy to observe that we can solve this problem by using the merge operation of Merge Sort.

Let's say we have two sorted arrays foo and bar of length fooLength and barLength, respectively. Next, we can declare another array merged of size fooLength + barLength.

We should then traverse both of the arrays in the same loop. We'll maintain a current index value for each, fooPosition and barPosition. On a given iteration of our loop, we take whichever array has the smaller-valued element at their index and advance that index. This element will occupy the next position in the merged array.

Finally, once we've transferred all elements from one array, we'll copy the remaining from the other into the merged array.

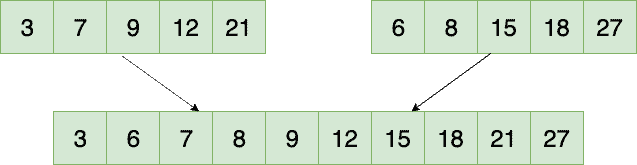
Now let's see the process in pictures to better understand the algorithm.

Step 1:

We start by comparing the elements in both the arrays, and we pick the smaller one.

Then we increment the position in the first array.

Step 2:

Here we increment the position in the second array and move on to the next element which is 8.

Step 3:

At the end of this iteration, we've traversed all the elements of the first array.

Step 4:

In this step, we just copy all the remaining elements from the second array to result.

4. Implementation

Now let's see how to implement it:

public static int[] merge(int[] foo, int[] bar) {

    int fooLength = foo.length;
    int barLength = bar.length;

    int[] merged = new int[fooLength + barLength];

    int fooPosition, barPosition, mergedPosition;
    fooPosition = barPosition = mergedPosition = 0;

    while(fooPosition < fooLength && barPosition < barLength) {
        if (foo[fooPosition] < bar[barPosition]) {
            merged[mergedPosition++] = foo[fooPosition++];
        } else {
            merged[mergedPosition++] = bar[barPosition++];
        }
    }

    while (fooPosition < fooLength) {
        merged[mergedPosition++] = foo[fooPosition++];
    }

    while (barPosition < barLength) {
        merged[mergedPosition++] = bar[barPosition++];
    }

    return merged;
}

And let's proceed with a brief test:

@Test
public void givenTwoSortedArrays_whenMerged_thenReturnMergedSortedArray() {

    int[] foo = { 3, 7 };
    int[] bar = { 4, 8, 11 };
    int[] merged = { 3, 4, 7, 8, 11 };

    assertArrayEquals(merged, SortedArrays.merge(foo, bar));
}

5. Complexity

We traverse both the arrays and choose the smaller element. In the end, we copy the rest of the elements from the foo or the bar array. So the time complexity becomes O(fooLength + barLength). We've used an auxiliary array to obtain the result. So the space complexity is also O(fooLength + barLength).

6. Conclusion

In this tutorial, we learned how to merge two sorted arrays into one.

As usual, the source code for this tutorial can be found over on GitHub.